Every Euler Circuit Is an Euler Path.

Therefore Euler circuits are a subset of Euler paths. Every complete graph that has a Hamilton circuit has at least one Euler circuit.

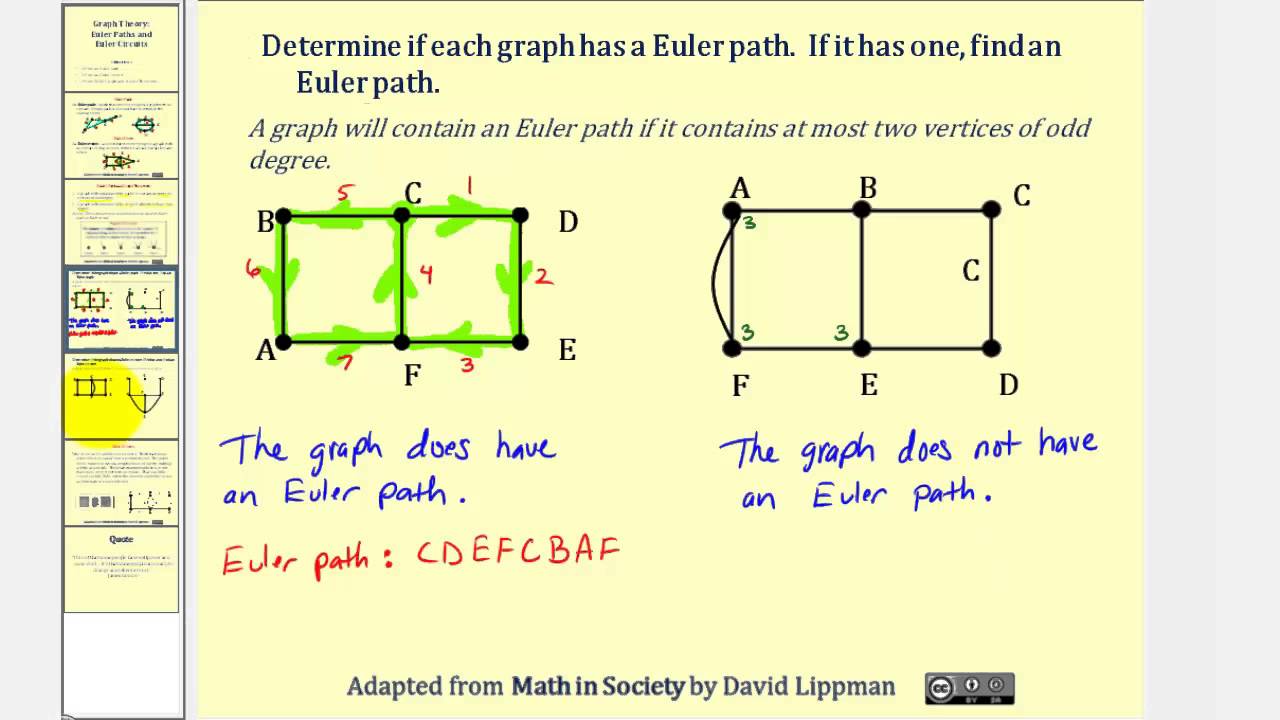
Graph Theory Euler Paths And Euler Circuits Youtube

Note that every Euler circuit is an Euler path but not every Euler path is an Euler circuit.

. An Euler circuit also begins and ends on the same vertex. Euler Circuit An Euler path that starts and ends at the same vertex Example 1 Euler Circuit One Euler circuit for the above graph is E A B F E F D C E as shown below. Our goal is to find a quick way to check whether a graph for multigraph has an Eder path or circuit 1.

All the vertices must be even for the graph to have an Euler circuit. Ad Over 27000 video lessons and other resources youre guaranteed to find what you need. A Euler circuit goes through every edge once and starts and ends at the same vertex.

Then every Euler path that starts at B must also end at B and is therefore an Euler circuittext From these two observations we can establish the following necessary conditions for a graph to have an Euler path or an Euler circuit. Test your knowledge on Euler and Hamilton Paths and Circuits with this amazing quiz and determine whether a graph has an Euler or a Hamilton path. The problem can be stated mathematically like this.

Is every Euler circuit an Euler path. The Euler Circuit is a special type of Euler path. If a graph has any vertices of odd degree then it cannot have.

When the starting vertex of the Euler path is also connected with the ending vertex of that path then it is called the Euler Circuit. An Euler circuit is an Euler path which starts and stops at the same vertex. Eulerian Circuit is an Eulerian Path which starts and ends on the same vertex.

Eulerian Path is a path in graph that visits every edge exactly once. Question Find any Euler paths Euler circuits Hamilton paths andor Hamilton circuits if possible in graph Ki below. An Euler circuit is an Euler path which starts and stops at the same vertex.

One such path is CABDCB. An Euler path in a graph or multigraph is a walk through the graph which uses every edge exactly once. The statement is true because both an Euler circuit and an Euler path are paths that travel through every edge of a graph once and only once.

First Euler Path Theorem. An Euler path in G is a simple path containing every edge of G. Every Euler circuit is an Euler path.

The Euler path is a path by which we can visit every edge exactly once. Euler paths and Euler circuits are used in the real world by postmen and salesmen when they are planning the best routes to take. Lecture 24 Euler and Hamilton Paths.

Every Euler path is an Euler circuit. Is a circuit that travels through every edge of a graph once and only once. A path that does not repeat vertices is called a simple path.

If a graph has an Euler path then. An Euler path is a path that uses every edge in a graph with no repeats. The path is shown in.

Similarly an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex. An Euler circuit in a graph G is a simple circuit containing every edge of G. An Euler circuit is a circuit in a graph where each edge is crossed exactly once.

Euler Paths and Euler Circuits An Euler Path is a path that goes through every edge of a graph exactly once An Euler Circuit is an Euler Path that begins and ends at the same vertex. In the graph shown below there are several Euler paths. Lecture 24 Euler and Hamilton Paths De nition 1.

An Euler path in a graph or multigraph is a walk through the graph which uses every edge exactly once. One such path is CABDCB. The path is shown in.

An Euler path in a graph or multigraph is a walk through the graph which uses every edge exactly once. An Euler path is a path that uses every edge in a graph with no repeats. If a graph has more.

An Euler path is a path in a graph that uses every edge exactly one time and it starts and ends at different vertices. Euler Path Euler Circuit Eulers Theorem. A Hamilton path is a path in a graph that uses every vertex exactly once and it begins and ends.

To detect the path and circuit we have to follow these conditions. In a weighted graph the lengths of the edges are proportional to their weights. In the graph shown below there are several Euler paths.

Being a path it does not have to return to the starting vertex. Therefore it is also an Euler circuit. Understand the definition of an Euler circuit.

This Euler path travels every edge once and only once and starts and ends at the same vertex. An Euler path or Euler circuit is a path or circuit that travels through every edge of a graph once and only once. Suppose we have an Euler path or circuit which starts at a vertex S.

Like all circuits an Euler circuit must begin and end at the same vertex. In graph theory an Eulerian trail is a trail in a finite graph that visits every edge exactly once. Did some research from Euler Paths and Circuits.

Eulers theorem provides a procedure for finding Euler paths and Euler circuits. We can use the same vertices for multiple times. Some graphs have no Euler paths.

The difference between a path and a circuit is that a circuit starts and ends at the same vertex a path doesnt. A circuit is path that begins and ends at the same vertex. An Euler path is a path that travels through all edges of a connected graph.

They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. A Euler path goes through every edge once. Being a path it does not have to return to the starting vertex.

A simple path in a graph G that passes through every vertex exactly once is called a Hamilton path and a simple circuit in a graph G that passes. The start and end points are the same. It must be connected and.

Our goal is to find a quick way to check whether a graph or multigraph has an Euler path or circuit.

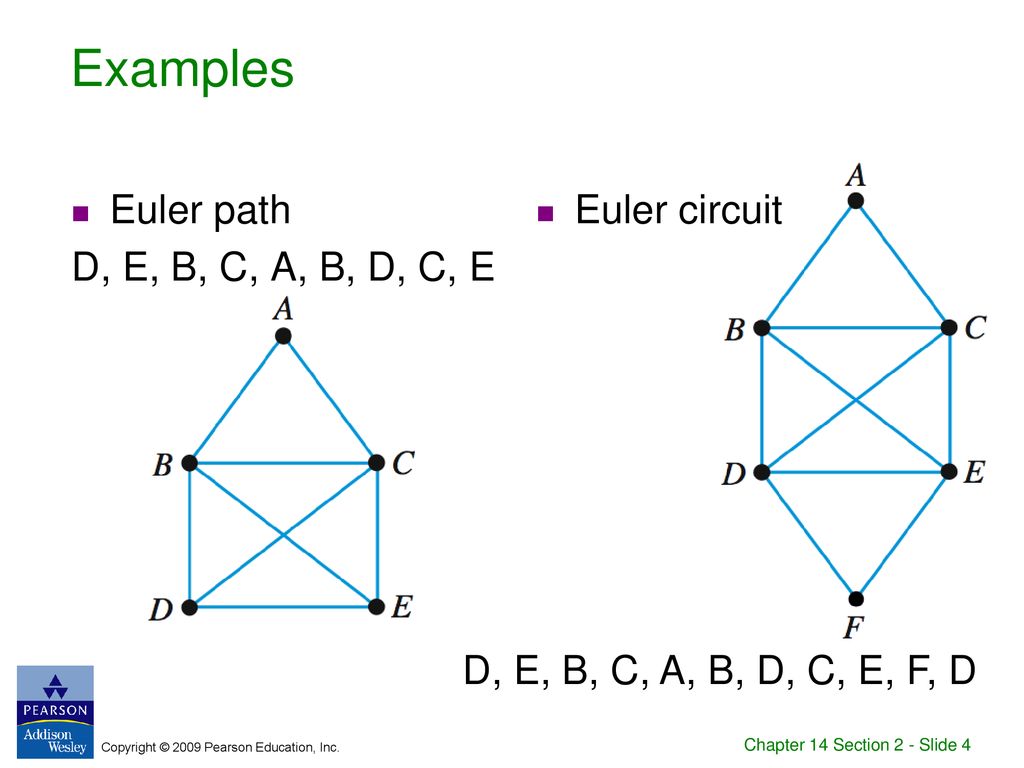
Euler Paths Euler Circuits Ppt Download

Euler Circuits And Paths Youtube

Euler Path And Euler Circuit Slaystudy